1.-TEORÍA DE MUESTRAS
1.1 Población y muestra
Entendemos por población un conjunto de elementos que poseen una característica o propiedad común, y que constituyen la totalidad de los individuos de interés para nuestro estudio.
En particular, nos interesa obtener información acerca de algún valor que caracteriza a la población, como una media, una varianza, una mediana, etc. A estos valores que se refieren a la totalidad de la población se les denomina parámetros poblacionales y en su notación es común utilizar el alfabeto griego:
μ (media poblacional), σ2 (varianza poblacional), σ (desviación típica poblacional), etc.
Como las poblaciones en las que se pretende estudiar una determinada variable aleatoria son grandes, es muy caro o imposible estudiar a todos sus individuos; lo que se hace, es estudiar una muestra (una parte) de la población :
Una muestra es cualquier subconjunto de la población sobre el que se realizan estudios para obtener conclusiones acerca de las características de la población.
Cualquier valor obtenido a partir de los datos de la muestra se denomina estadístico muestral. Ejemplos de estadísticos muestrales son:
- \(\overline{x}\) (media muestral),
- S 2 (varianza muestral),
- S (desviación típica muestral), etc.
Si por ejemplo decimos que la duración media de las bombillas que fabrica un empresa es de 1600 horas, nos referimos a la población y la media la designamos por µ = 1600. Sin embargo si hallamos la duración media de una muestra de 20 bombillas y obtenemos 1580 horas, nos referimos a la muestra y la media la designamos por $ \overline x = 1580 $.
Podrıamos a continuación hallar la duración media de otra muestra de 30 bombillas y obtener 1610 horas, nos referimos a la muestra y la media la designamos por $ \overline x = 1610 $ . La media muestral (de las muestras) es una variable aleatoria mientras que la media poblacional es una constante.
• La media µ de la población es un parámetro y es constante.
• La media $ \overline {x } $ de la muestra es un estadístico y es una variable aleatoria
La teoría del muestreo tiene por objetivo, el estudio de las relaciones existentes entre la distribución de un carácter en dicha población y las distribuciones de dicho carácter en todas sus muestras.
Las ventajas de estudiar una población a partir de sus muestras son principalmente:
- Coste reducido:
- Si los datos que buscamos los podemos obtener a partir de una pequeña parte del total de la población, los gastos de r ecogida y tratamiento de los datos serán menores. Por ejemplo, cuando se realizan encuestas previas a un referéndum, es más barato preguntar a 4.000 personas su intención de voto, que a 30.000.000;
- Mayor rapidez:
- Estamos acostumbrados a ver cómo con los resultados del escrutinio de las primeras mesas electorales, se obtiene una aproximación bastante buena del resultado final de unas elecciones, muchas horas antes de que el recuento final de votos haya finalizado;
- Más posibilidades:
- Para hacer cierto tipo de estudios, por ejemplo el de duración de cierto tipo de bombillas, no es posible en la práctica destruirlas todas para conocer su vida media, ya que no quedaría nada que vender. Es mejor destruir sólo una pequeña parte de ellas y sacar conclusiones sobre las demás.
De este modo se ve que al hacer estadística inferencial debemos enfrentarnos con dos problemas:
- Elección de la muestra (muestreo).
- Extrapolación de las conclusiones obtenidas sobre la muestra, al resto de la población (inferencia).
Es decir, el principal objetivo de la mayoría de los estudios, análisis o investigaciones, es hacer generalizaciones “acertadas” con base en muestras de poblaciones de las que se derivan tales muestras. Obsérvese la palabra “acertadas” porque no es fácil responder cuándo y en qué condiciones las muestras permiten tales generalizaciones.
Por ejemplo si queremos calcular la cantidad de dinero que se gasta una persona en vacaciones, ¿tomaríamos como muestra lo que gastan los viajeros que lo hacen en primera clase? Es obvio que no, pero saber a que tipo de personas debemos incluir en nuestra muestra no es algo intuitivo ni evidente.
Sobre las muestras hay dos aspectos que resultan fundamentales: el tamaño (nº de elementos de la muestra) y la forma en que se realiza la selección de los individuos que la forman.
La elección de la muestra influirá de manera determinante en los resultados, por lo que hay que evitar muestras “sesgadas” (parciales y subjetivas) que produzcan errores incontrolables (aparte de los errores propios de sustituir el estudio de una población por el de una muestra).
El tipo de muestreo más importante es el muestreo aleatorio, en el que todos los elementos de la población tienen la misma probabilidad de ser extraídos; Aunque dependiendo del problema y con el objetivo de reducir los costes o aumentar la precisión, otros tipos de muestreo pueden ser considerados como veremos a continuación.
2.- TIPOS DE MUESTREO
2.1. Muestreo Aleatorio Simple
Es la técnica de muestreo en la que todos los elementos que forman el universo y que, por lo tanto, están descritos en el marco muestral, tienen idéntica probabilidad de ser seleccionados para la muestra.
Consiste en seleccionar n elementos sin reemplazamiento de entre los N que componen la población, de tal modo que todas las muestras tengan la misma probabilidad de ser elegidas.
Es algo así como hacer un sorteo justo entre los individuos del universo: asignamos a cada persona un boleto con un número correlativo, introducimos los números en una urna y empezamos a extraer al azar boletos. Todos los individuos que tengan un número extraído de la urna formarían la muestra. Obviamente, en la práctica estos métodos pueden automatizarse mediante el uso de ordenadores.
En la práctica, se enumeran los individuos y se sortean cuáles de ellos se elegirán. Si los individuos son, por ejemplo, tornillos que se encuentran en una caja, se eligen al azar por simple extracción.
2.2 Muestreo Aleatorio Sistemático
Se numeran los individuos y, a partir de uno de ellos elegido al azar, se toman los siguientes mediante “saltos” numéricos iguales. El salto se llama coeficiente de elevación, k, y se obtiene mediante el cociente entero entre el número de individuos de la población, N y el número de individuos de la muestra: n −>k = N/n. El primer elemento, llamado origen, se elige al azar entre los números 1,2,3,....,k. Esta forma de muestreo sólo es válida si el criterio por el que se han numerado los individuos de la población no tiene nada que ver con la característica que se quiere estudiar con la muestra..
\(\LARGE k=\frac{N \;de \;elementos\; de\; la\; pobación}{Tamaño\; de\; la\; muestra}=\frac{N}{n}\)
Por ejemplo:
Si tenemos una población formada por 100 elementos y queremos extraer una muestra de 25 elementos, en primer lugar debemos establecer el intervalo de selección que será igual a 100/25=4. A continuación elegimos el elemento de arranque, tomando aleatoriamente un número entre el 1 y el 4, y a partir de él obtenemos los restantes elementos de la muestra:
2 , 6 , 10 , 14 , … , 98
2.3.-Muestreo Aleatorio Estratificado
Si conocemos que la población puede dividirse en partes o estratos, en relación con variables que pueden ser de interés en nuestro estudio, de modo que en cada uno de los estratos los elementos posean una gran homogeneidad respecto al carácter que se estudia (sexo, grupos de edad, nivel de estudios,…), se puede aumentar la precisión si muestreamos los estratos por separado. La forma de repartir los elementos de la muestra, determinando cuantos deben corresponder a cada estrato se denomina afijación , y puede ser de varios tipos:
- Afijación uniforme : Si se toma el mismo número de elementos en cada estrato.
\(n_1=n_2=...=n_k=\frac{n}{k}\)
- Afijación Proporcional : si el número de elementos que se toma en cada estrato es proporcional al tamaño del estrato. Se utiliza cuando las varianzas de los estratos no difieren mucho entre si.
\(\frac{n_1}{N_1}=\frac{n_2}{N_2}=...=\frac{n_k}{N_k}=\frac{n}{N}\)
Ejemplo:
Por ejemplo, queremos estudiar el % de la población que fuma en México y pensamos que la edad puede ser un buen criterio para estratificar (es decir, pensamos que existen diferencias importantes en el hábito de fumar dependiendo de la edad). Definimos 3 estratos: menores de 20 años, de 20 a 44 años y mayores de 44 años. Es de esperar que al dividir toda la población mexicana en estos 3 estratos no resulten grupos de igual tamaño. Efectivamente, si miramos datos oficiales, obtenemos:
* Estrato 1 - Población Mexicana menor de 19 años: 42,4 millones (41,0%)
* Estrato 2 - Población Mexicana de 20 a 44 años: 37,6 millones (36,3%)
* Estrato 3 - Población Mexicana mayor de 44 años: 23,5 millones (22,7%)
Si usamos muestreo estratificado proporcionado, la muestra deberá tener estratos que guarden las mismas proporciones observadas en la población. Si en este ejemplo queremos crear una muestra de 1.000 individuos, los estratos tendrán que tener un tamaño como sigue:
| Estrato | Población | Proporción | Muestra |
| 1 | 42,4M | 41,0% | 410 |
| 2 | 37,6M | 36,3% | 363 |
| 3 | 23,5M | 22,7% | 227 |
Hablaremos de una afijación uniforme cuando asignamos el mismo tamaño de muestra a todos los estratos definidos, sin importar el peso que tienen esos estratos en la población. Siguiendo con el ejemplo anterior, un muestreo estratificado uniforme definiría la siguiente muestra por estrato:
| Estrato | Población | Proporción | Muestra |
| 1 | 42,4M | 41,0% | 334 |
| 2 | 37,6M | 36,3% | 333 |
| 3 | 23,5M | 22,7% | 333 |
Ejemplo 2
En una ciudad se quiere hacer un estudio para conocer qué tipo de actividades se realizan en el tiempo dedicado al ocio. Para ello van a ser encuestadas 300 personas elegidas al azar mediante muestreo aleatorio estratificado con afijación proporcional. Teniendo en cuenta que de un total de 15.000 habitantes, 7.500 son adultos, 3.000 ancianos y 4.500 niños, definir los estratos y el tamaño muestral correspondiente a cada estrato.
Solución:
Basta con hacer una simple regla de 3 para determinar el tamaño muestral de cada estrato:
Niños:
15.000---------4500
300 ------------- x
x=(4.500 * 300)/1500=90 niños
Adultos:7.500 * 300/15000=150 adultos
Ancianos:3.000 * 300/15000=90 ancianos
2.4.-Muestreo Por Conglomerados o áreas
En este tipo de muestreo, llamado muestreo por conglomerados, se divide la población total en un número determinado de subdivisiones relativamente pequeñas y se seleccionan al azar algunas de estas subdivisiones o conglomerados, para incluirlos en la muestra total. Si estos conglomerados coinciden con áreas geográficas, este muestreo se llama también muestreo por áreas .
Por ejemplo, supongamos que una gran empresa quiere estudiar los patrones variables de los gastos familiares de una ciudad como Granada. Al intentar elaborar los programas de gastos de una muestra de 1200 familias, nos encontramos con la dificultad de realizar un muestreo aleatorio simple, (es complicado tener una lista actualizada de todos los habitantes de una ciudad). Una manera de tomar una muestra en esta situación es dividir el área total ( Granada en este caso) en áreas más pequeñas que no se solapen (Por ejemplo Distritos postales, manzanas etc...) En este caso seleccionaríamos algunas áreas al azar y todas las familias (o muestras de éstas) que residen en estos distritos postales o manzanas, constituirían la muestra definitiva.
Aunque las estimaciones basadas en el muestreo por conglomerados, por lo general no son tan fiables como las obtenidas por muestreos aleatorios simples del mismo tamaño, son más baratas. Volviendo al ejemplo anterior, es mucho más económico visitar a familias que viven en el mismo vecindario, que ir visitando a familias que viven en un área muy extensa.
En la práctica se pueden combinar el uso de varios de los métodos de muestreo qu e hemos analizados para un mismo estudio.
Ejemplo
Se estudia la incidencia de enfermedades cardíacas en la población rural española. Para ello se hace un censo de pueblos y se eligen varios al azar, donde se estudia a la población
Ejercicios:
1.- Consideremos la población formada por 5 bolas contenidas en una urna y numeradas del 1 al 5. Obtener todas las muestras de tamaño 2 extraídas mediante muestreo aleatorio simple.
2.- En un instituto de enseñanza secundaria en que se ofertan los siguientes tipos de enseñanza :
- Ciclos de grado superior: 110 alumnos.
- Bachillerato: 162 alumnos.
- Ciclos de grado medio : 210 alumnos
- 2º ciclo de enseñanza secundaria obligatoria: 338 alumnos.
Se pretende valorar las faltas de ortografía que cometen los alumnos del centro mediante una prueba-dictado de un texto de 20 líneas; la prueba se pasará a una muestra de 50 alumnos, para minimizar el costo en tiempo y medios.
¿Cómo se obtiene una muestra adecuada a esta población?
Solución :En esta situación parece conveniente utilizar para la extracción de la muestra el muestreo aleatorio estratificado con afijación proporcional. Dividimos la población en cuatro estratos: ciclos de grado superior, ciclos de grado medio, bachillerato y 2º ciclo de enseñanza secundaria obligatoria.
Como el número total de alumnos son 820 y la muestra debe estar formada por 50 alumnos, el cálculo del número de alumnos que se han de tomar de cada estrato es:
Ciclos de grado superior:
820 -----110
50 -----x $ x=\frac{50 ·110}{820}=7 $
Bachillerato:
820 ----162
50 -----x $ x=\frac{50 ·162}{820}=10 $
Ciclos de grado medio:
820 ----210
50 -----x $ x=\frac{50 ·210}{820}=13 $
2º ciclo de Enseñanza Secundaria Obligatoria:
820 ----338
50 --------x $ x=\frac{50 ·338}{820}=20 $
Los empleados de una empresa están clasificados como figura en la siguiente tabla :
| Categoría | A | B | C | D |
|---|---|---|---|---|
| Nº de empleados | 500 | 300 | 350 | 150 |
Para hacer una consulta sobre la modificación del horario laboral, se elige por sorteo a 40 empleados de la categoría A, 30 de la B, 50 de la C y 20 de la D.
¿Es este un modelo de muestreo aleatorio estratificado? ¿Es proporcional?
Es un muestreo aleatorio estratificado pero no proporcional ya que
$ \frac{40}{500}\neq\frac{30}{300}\neq\frac{50}{350}\neq\frac{20}{150} $
Si quisieramos que fuera proporcional con una muestra de 140
$ \frac{A}{500}=\frac{B}{300}=\frac{C}{350}=\frac{D}{150}=\frac{140}{300} \Rightarrow A=54;B=32;C=38;D=16 $
En un centro, hay 2000 alumnos, 720 en 3º de ESO, 700 en 4º de ESO, 340 en 1º de Bachillerato, y 240 en 2º de Bachillerato. Si deseamos tomar una muestra de 100 alumnos, para conocer la opinión que tiene el alumnado sobre una medida que ha tomado el Consejo Escolar, ¿cómo elegirías una muestra de 100 alumnos por muestreo aleatorio estratificado?
Solución: 3º de ESO: 36 alumnos; 4º de ESO: 35 alumnos; 1º de Bachillerato: 17 alumnos; 2º de Bachillerato: 12
alumnos.
Tamaño y representatividad de una muestra
Cuando se elige una muestra los dos aspectos que hay que tener en cuenta son, el tamaño y la representatividad de la muestra.Si la muestra es demasiado pequeña, aunque esté bien elegida, el resultado no será fiable.
Ejemplo:
Queremos estudiar la estatura de la población española. Para ello elegimos a una persona al azar y la medimos.
Evidentemente este resultado no es fiable. La muestra es demasiado pequeña.
Si la muestra es demasiado grande los resultados serán muy fiables, pero el gasto puede ser demasiado elevado. Incluso, en ocasiones, muestras demasiado grandes no nos proporcionan mejores resultados. Vamos a aprender a encontrar cuál es el tamaño adecuado para que podamos afirmar que la población tiene tal característica con una probabilidad dada, grande.
Cuando una muestra tenga el tamaño adecuado, y haya sido elegida de forma aleatoria diremos que es una muestra representativa.
Si la muestra no ha sido elegida de forma aleatoria diremos que la muestra es sesgada.
Ejemplo:
Indica si es población o muestra:
- En una ganadería se mejora el pienso de todas las ovejas con un determinado tipo de grano.
- En otra ganadería se seleccionan 100 ovejas para alimentarlas con ese tipo de grano y estudiar su eficacia.
En el primer caso, todas las ovejas, son la población. En el segundo se ha elegido una muestra.
En una serie de televisión tienen dudas sobre qué hacer con la protagonista, si que tenga un accidente o si debe casarse. Van a hacer una consulta. ¿A toda la población o seleccionado una muestra representativa?
Observa que no sabemos bien cuál sería la población, ¿los que ven esa serie? o ¿toda la población española? Si son los que ven la serie, ¿cómo los conocemos? ¿Cómo preguntar a todos? Parece más operativo preguntar a una muestra.
El estudio de la vida media de unas bombillas, ¿se puede hacer sobre toda la población?
El estudio es destructivo. Si se hiciera sobre toda la población nos quedamos sin bombillas. Es imprescindible tomar una muestra.
Disponemos del censo electoral de una población. Consta de 33.600 electores. Deseamos extraer una muestra de 300 individuos.
a) ¿Cómo se debe realizar mediante muestreo aleatorio sistemático?
b) ¿Cómo se debe realizar mediante muestreo aleatorio simple?
Solución
a)Coeficiente de elevación : $ h = \frac{ 33600}{ 300} = 112 $
Esto significa que hemos de seleccionar un individuo de cada 112. Elegimos al azar un número del 1 al 112. El segundo elemento será n + 112, y asi sucesivamente.
b)Habrá que seleccionar un individuo al azar de entre los 33600, descartando a a quellos que salgan repetido. Este proceso habrá que repetirlo 300 veces, que es el tamaño de mi muestra.
3.-DISTRIBUCIÓN DE LAS MEDIAS MUESTRALES
De una población se selecciona una muestra y se calcula su media $ \overline {x} $ y su desviación típica, s.
Elegimos otras muestras de la misma población, y de cada una obtenemos su media y desviación típica.
¿Cómo es la distribución de esas medias? ¿Y de esas desviaciones típicas?
Las diferentes medias dan lugar a una variable aleatoria que la vamos a representar por \(\overline {X}\) .
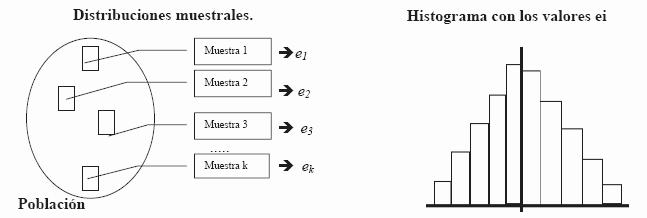
La idea de distribución muestral es la siguiente:
Partimos de una población de tamaño N. Obtenemos k muestras (todas las posibles de tamaño n) y de cada una de ellas se calcula una medida (media, mediana, varianza, desviación típica,..) obteniendo k valores: e1 , e2 , e3 ,...ek .
Estos valores pueden representarse mediante un histograma para observar su distribución:
Se puede observar que este histograma va adquiriendo forma de campana de Gauss, y a medida que k aumenta, se va pareciendo cada vez más a la forma de una distribución Normal.
Lo vemos con un ejemplo:
Elaboraremos la distribución muestral de la media de una muestra aleatoria de tamaño n = 2 tomada sin reemplazo de la población finita de tamaño N = 5, cuyos elementos son: 3,5,7,9,11.
\( \mu =\frac{3+5+7+9+11}{75}=7\)
\(\sigma ^2 =\frac{3^2+5^2+7^2+9^2+11^2}{75}- 7^2=8 ⇒\sigma =\sqrt{8}\)
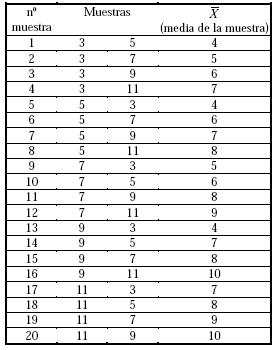
Ahora si tomamos una muestra aleatoria de tamaño n = 2 de esta población hay 20 posibilidades:
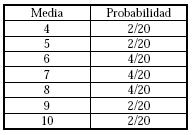
Si hacemos la función de probabilidad de la variable \(\overline{X}\) de las medias muestrales:
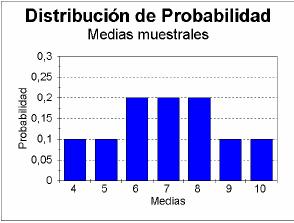
Cuyo histograma sería:
Si calculamos la media y la desviación típica de la distribución de las medias obtenemos
que: \(\mu_ {\overline{x} }= 7\) y \( \sigma_{ \overline{x} }=\sqrt{ 3}\), luego la media \(\mu_x\) coincide con la media de la población y la desviación típica ha disminuido.
Este ejemplo puede generalizarse para cualquier distribución según el siguiente teorema:
Teorema Central del Límite
Si una población tiene media μ y desviación típica σ, y tomamos muestras de tamaño n (n>30, ó cualquier tamaño si la población es "normal"), las medias de estas muestras siguen aproximadamente la distribución:
\[ \overline{X} \longrightarrow N( \mu ,\frac{ \sigma}{ \sqrt{n}})\]
Destacar que si la población de la que se obtienen las muestras es normal, las medias muestrales también se distribuyen según una distribución normal, independientemente del tamaño de la muestra.
Al saber cómo funcionan las medias muestrales, podemos obtener probabilidades relacionadas con ellas.
Ejemplo
Se sabe que las bolsas de azúcar producidas por una máquina tiene una media de 500 g. y una desviación típica de 35 g. Dichas bolsas se empaquetan en cajas de
100 unidades.
a) ¿Cómo se distribuyen las medias de los pesos de las bolsas de cada caja?
b) Calcular la probabilidad de que la media de los pesos de las bolsas de un paquete sea inferior a 495 g.
- Tenemos \( \mu=500 , \sigma =35 , n = 100\);
Por el Teorema Central del Límite (aunque la variable peso no sea normal, tenemos n > 30), la variable X = “media de los pesos de la muestra” se distribuye según una normal:
\(\overline{X} \longrightarrow N( \mu ,\frac{ \sigma}{ \sqrt{n})}= N( 500 ,\frac{ 35}{ \sqrt{100})}=N(500,3'5)\)
P(\(\overline{X}<495\) )=tipificando=P(\(\frac{\overline{X}-500}{3'5}< \frac{495-500}{3'5}\) )=P(Z<-1'43)=P(Z<1'43)=1-P(Z<1'43)=0,0764
Lo que vendría a significar que en el 7’6 % de las cajas el peso medio de las bolsas es inferior a 495 g.
Ejemplo
Los parámetros de una distribución son \(\mu = 10\) y desviación típica \(\sigma = 2\). Se extrae una muestra de 100 individuos. Calcula P(8 < \(\oveline{X}\) < 12).
Por el teorema Central del Límite sabemos que la media muestral de una población normal se distribuye mediante otra distribución normal \(N( \mu , \sigma)\)
\(P(8<\overline{X}<12)=tipificando=P(\frac{8-10}{2/10}<\frac{\overline{X}-10}{2/10}< \frac{8-10}{2/10})=\)
\(=P(-1<Z<1)=2P(Z<1)-1=2(0,8416)-1=0,6832\)
Ejemplo
Las estaturas, en centímetros, de un grupo de soldados se distribuyen normalmente con media 173 y desviación típica 6.
a) Elegido un soldado al azar, ¿cuál es la probabilidad de que mida menos de 175 cm.?
b) Si se toma una muestra de 12 soldados, ¿cuál es la probabilidad de que su estatura media supere el 1’76?
Solución:
a) Cuidado, en este apartado no hay muestra, ni por tanto medias muestrales, sino un simple ejercicio de la normal.
Si X = “altura”, sabemos que sigue una \(N(173,6)\)
Luego
P(\(\overline{X}<175\))=tipificando=P(\(\frac{\overline{X}-173}{6}< \frac{175-173}{6}\))=P(Z<0,33)=0,6293
Aquí si tenemos una muestra con n=12
Aunque sea $ n < 30 $ , como la población de partida es normal, podemos también aplicar el Teorema Central del Límite:
$ \overline{X} \longrightarrow N( \mu ,\frac{ \sigma}{ \sqrt{n})}= N( 173 ,\frac{ 6}{ \sqrt{12})}=N(173,1'73) $
Luego
$ P(\overline{X}>176) $ =tipificando= $ P(\frac{\overline{X}-173}{1,73}< \frac{175-173}{1,73})=P(Z>1,73)=1-P(Z<1,73)=1-0'9582=0,0418 $
Ejemplo
Una compañía aérea sabe que el equipaje de sus pasajeros tiene como media 25 kg. con una desviación típica de 6 kg. Si uno de sus aviones transporta a 50 pasajeros, el peso medio de los equipajes de dicho grupo estará en la distribución muestral de medias:
N(25, $ \frac{6} {\sqrt{50}})= N (25; 0,84) $
La probabilidad de que el peso medio para estos pasajeros sea superior a 26 kg sería:
P( $ \overline{x}>26 $ )=tipificando=P( $ \frac{\overline{X}-25}{0,84}> \frac{26-25}{0,84})=P(Z>1,18)=1-P(Z<1,18)=0,1190=11,90 \% $
Ejemplo
En el control de calidad de una fábrica de latas de atún, se embasan latas de 100 gramos con una desviación típica de 2 gramos. Se empaquetan en cajas de 50 latas. Calcula la probabilidad de que la media de las latas de una caja sea menor que 99 gramos.
Los datos que nos dan son la media poblacional, $ \mu = 100 $ , la desviación típica poblacional, $ \sigma= 2 $ , y el tamaño de la muestra, n = 50.
Sabemos que la media muestral se distribuye según una $ N(\mu,\frac{\sigma}{\sqrt{n}})=N(100,\frac{2}{\sqrt{50}})=N(100,0,28) $
Vamos a recordar como calculábamos esas probabilidades.
Queremos calcular P( $ \overline{x} $ < 99).
Lo primero tipificamos para pasar a una distribución N(0, 1).
P( $ \overline{x}<99 $ )=tipificando=P( $ \frac{\overline{X}-100}{0,28}< \frac{99-100}{0,28} $ )=P(Z<-3,54)=1-P(Z<3,54)
Recuerda:
La distribución normal es simétrica, por eso en la tabla no aparecen valores negativos, pues los calculamos usando los positivos. Buscamos en la tabla 3’54 y obtenemos que P(z < 3’54) = 0’9998.
$ P( \overline{x}<99)) = 1 - P(z < 3’54) = 1 - 0’9998 = 0’0002 $ , una probabilidad muy pequeña.
. Control de la suma de todos los individuos de la muestra
Si tomamos una muestra aleatoria simple de tamaño n de una variable aleatoria X: X1, X2, ..., Xn con media μ y desviación típica σ , entonces la variable aleatoria X = X1 + X2+ ... + Xnpara n suficientemente grande (![]() ) la distribución muestral de medias X se aproxima a una distribución normal:
) la distribución muestral de medias X se aproxima a una distribución normal:
Media: $ n \mu $
Desviación típica: $ \sigma \sqrt{n} $
X=N( $ n \mu $ , $ \sigma \sqrt{n} $ )
Ejemplo
Control de la suma: En el mismo ejemplo anterior determina la probabilidad de que un lote de 400 latas pese más de 40100 gramos.
Como la media muestral es igual a $ \overline{x}=\frac{\sum\limits_{i=1}^n{x_i}}{n} $ entonces $ n \overline{x}=\sum\limits_{i=1}^n{x_i} $
por lo que su distribución es una normal de media $ n \mu $ y desviación típica $ \sigma = n \frac{ \sigma }{ \sqrt{n} }=\sigma \sqrt{n}:N(n \mu , \sigma \sqrt{n}) $
En nuestro caso N( $ n \mu $ , $ \sigma \sqrt{n} $ ) = N(400×100, 2 $ \sqrt{400} $ ) = N(40000, 40)
Queremos calcular
$ P(\sum\limits_{i=1}^n{x_i}>40100)=P(Z>\frac{40100-40000}{40}=P(Z<2,5)1-P(Z<2,5)=1-0,9938=0,0062 $
Unas 6 cajas de cada mil pesarán más de 40’1 kg.
El voltaje de las baterías de un fabricante es de 12 voltios de media y con una desviación típica de 0,3 voltios. Elegimos al azar 5 de esas baterías y se conectan en seria, lo que supone que se suman los voltajes. Calcula la probabilidad de que tengan un voltaje conjunto de más de 61 voltios.
Solución :El voltaje del conjunto de las baterias sigue una distribución con la siguiente expresión:
X=sumatorio de las medias de la muestra
X=N( $ n \mu $ , $ \sigma \sqrt{n} $ ) = N(5×12, 0,3 $ \sqrt{5} $ ) = N(60, 0,67)
$ P(\sum\limits_{i=1}^n{x_i}>61)=P(X>61)=P(Z>\frac{61-60}{0,67}=P(Z>1,49)=1-P(Z<1,49)=1-0,9319=0,0681 $
Ejercicios:
- Se supone que la distribución de la temperatura del cuerpo humano en la población tiene de media 37º y de desviación típica 0’85º. Se elige una muestra de 105 personas. Hallar las probabilidades de que:
- La media sea menor que 36’9º
- La media esté comprendida entre 36’5º y 37’2º
- Las notas de cierto examen se distribuyen según una normal de media 5,8 y desviación típica 2,4. Hallar la probabilidad de que la media de una muestra tomada al azar de 16 estudiantes esté comprendida entre 5 y 7
- Consideremos la población formada por los cuatro elementos 0, 3, 4, 6. Hallar:
- Todas las muestras posibles de tamaño 2 extraídas mediante muestreo aleatorio simple
- La media y la desviación típica poblacionales
- La media y la desviación típica de las medias muestrales
- Los pesos de las ovejas de una cierta ganadería tienen una media de 50 kg con una desviación típica de 4. Elegimos al azar una muestra aleatoria simple de 100 ovejas.
- Determina la probabilidad de que su media sea superior a 51 kg.
- Sea inferior a 56 kg.
- Sea superior a 48 kg.
- Esté entre 48 kg y 52 kg.
- Una población tiene una media $ \mu $ = 400 y una desviación típica = 20. Extraemos una muestra de 1000 individuos. Halla el intervalo característico, para una probabilidad de 0’95, de la media muestral. Lo mismo para una probabilidad del 0’99.
- El peso de una población se estima que tiene de media $ \mu $ = 70 kg y una desviación típica = 10. Se elige una muestra aleatoria simple de 100 individuos y se pesan todos juntos. Calcula la probabilidad de que dicho peso sea superior a 7010 kg.
4.-DISTRIBUCIÓN DE LAS PROPORCIONES MUESTRALES
Hemos estudiado el curso pasado la distribución binomial. Era una situación en que las únicas posibilidades eran “éxito” y “no éxito”. Queremos saber cómo se distribuye la proporción muestral (número de éxitos entre el número de veces que se repite el experimento). Cada muestra que obtengamos de tamaño n se distribuye según una distribución binomial B(1, p), por tanto la suma de n variables B(1, p) es una binomial B(n, p) por el principio de reproductividad de la distribución.
En lugar de calcular medias de las muestras, ahora vamos a trabajar con proporciones.
En una población, la proporción de individuos que poseen una determinada característica es p. (Llamaremos q = 1 – p)
Extraemos todas las posibles muestras de tamaño n que podemos extraer de esa población. La proporción de individuos de cada una de esas muestras con esa característica ser $ \hat{p} $ . Llamaremos $ \hat{ P} $ a la variable aleatoria que toma los distintos valores de esas proporciones muestrales.
Si n es lo suficientemente grande (n > 30), se puede demostrar que la variable \(\hat{ P}\) sigue una distribución normal de parámetros:
\[ \hat{P} \Longrightarrow N(p , \sqrt{\frac{pq}{n}}) \]
(Esta fórmula proviene de la aproximación de una binomial por una normal)
Ejemplo 1:
Una nueva droga ha curado al 85% de los enfermos a los que se les ha aplicado. Si se toman muestras de 30 personas, ¿Cuál es la distribución de las
proporciones muestrales? ¿Y si las muestras son de 100 personas? ¿Y si son de 1000?
Solución:
Tenemos p = 0’85, por lo que q = 0’15
Si n=30
\[ \hat{P} \longrightarrow N(p , \sqrt{\frac{pq}{n}})=\hat{P} \longrightarrow N(0,85 , \sqrt{\frac{0,85 0,15}{30}}= \hat P=N(0,85,0,065)\]
Si n=100
\[ \hat{P} \longrightarrow N(p , \sqrt{\frac{pq}{n}})=\hat{P} \longrightarrow N(0,85 , \sqrt{\frac{0,85 0,15}{100}})= \hat P=N(0,85,0,036)\]
Si n=1000
\[\hat{P} \longrightarrow N(p , \sqrt{\frac{pq}{n}})=\hat{P} \longrightarrow N(0,85 , \sqrt{\frac{0,85 0,15}{1000}})= \hat P=N(0,85,0,011)\]
Como ya vimos con las medias muestrales, al aumentar el tamaño de las muestras disminuye la varianza de las distribuciones muestrales.
Ejemplo
Se sabe que el 15 % de los jóvenes entre 18 y 25 años son miopes.
- ¿Cómo se distribuye la proporción de jóvenes miopes en muestras de 40 individuos?
- ¿Cuál es la probabilidad de que en dicha muestra la proporción de miopes esté entre el 8 y el 22 %?
Solucion
Tenemos p = 0’15, por lo que q = 0’85. Además n = 40. Por tanto:
\[ \hat{P} \longrightarrow N(p , \sqrt{\frac{pq}{n}})=\hat{P} \longrightarrow N(0,15 , \sqrt{\frac{0,15 0,85}{40}})= \hat P=N(0,15,0,0565)\]
Usando el apartado anterior:
P(0,08<\(\hat {P}\)<0,22)=tipificando =P(\( \frac{0,08-0,15}{0,0565}<\hat{P}< \frac{0,22-0,15}{0,0565}\))=>P(\(-1,24 <Z<1,24\))=0,785
Esto significaría que en el 78’5 % de las muestras que extrajésemos de tamaño 40, la proporción de individuos miopes estaría entre el 8 y el 22%.
Ejemplo
El 42% de los habitantes de un municipio es contrario a la gestión del alcalde y el resto son partidarios de este. Si se toma una muestra de 64 individuos, ¿cuál es la probabilidad de que ganen los que se oponen al alcalde?
Solución:
Hay que hallar la probabilidad de que la proporción de la muestra sea superior al 0.5, es decir \(\hat{p }=\frac{x}{64}> 0.5\) o equivalentemente, que el número de los que se oponen en la muestra sea \(x > 0.5 * 64 = 32\)
Otra manera sería. En una muestra de 64 individuos x son los que se oponen. Para que ganen los que se oponen, x tiene que ser al menos la mitad de los
votos mas uno, es decir x ≥ 33. Siendo n = 64 µ = np = 26.88 σ = \( \sqrt{n · p · q} =\sqrt{64 · 0.42 · 0.58} = 3.95\)
Calculamos P(X ≥33) aproximando a la distribución normal, x ∼ N(26.88; 3.95);P(X ≥33) =1 − P(X ≤ 32)=1 − P(z <\( \frac{32.5 − 26.88}{3.95}\)==1 − Φ (1.42) ≈ 0.0778
EJERCICIOS
- Una máquina fabrica piezas de precisión y en su producción habitual tiene un 3% de piezas defectuosas. Se empaquetan en cajas de 200, ¿cuál es la probabilidad de encontrar entre 5 y 7 piezas defectuosas en una caja?
- Si tiramos una moneda no trucada 100 veces, ¿cuál es la probabilidad de que obtengamos más de 55 caras?
- Se ha realizado una encuesta a 20.000 universitarios sobre su actitud ante el botellón. De ellos, 13.200 son partidarios y el resto no. Se toman 100 muestras de 30 universitarios cada una. Hallar:
- La distribución de la proporción muestral de partidarios del botellón
- La probabilidad de que en una de estas muestras se manifiesten favorables al botellón más de 21 alumnos
- ¿En cuántas muestras cabe esperar que más de 15 y menos de 19 estudiantes se muestren partidarios del botellón?
- En el instituto de cierta localidad se imparten 4 niveles diferentes: 1º, 2º, 3º y 4º ESO, estando matriculados un total de 800 alumnos. En 1º hay 160 alumnos, en 2º hay 240 y en 3º hay 208. Explica cómo obtener una muestra de 50 alumnos mediante:
- Muestreo aleatorio sistemático
- Muestreo aleatorio estratificado con afijación proporcional
- En un barrio hay 4000 habitantes, distribuidos en cuatro urbanizaciones: el 12% viven en A, el 20% en B, el 36% en C y el 32% en D. Además, los porcentajes de mujeres en cada urbanización son: 50, 60, 66 y 75 % respectivamente. Se desea obtener una muestra de 50 habitantes que sea representativa en cuanto al sexo y a las urbanizaciones mediante muestreo aleatorio estratificado proporcional. ¿Cuántas personas (hombres y mujeres) de cada urbanización habrá que seleccionar?
- Dada la población {2, 4, 6 , 8}:
- Escribir todas las muestras posibles de tamaño 2 mediante muestreo aleatorio simple
- Calcular la media y la varianza de las medias muestrales
- Hacer lo mismo con todas las muestras posibles de tamaño 3
- La media de edad de los lectores de una determinada revista es de 17’2 años y la desviación típica de 2’3 años. Si elegimos muestras de 100 lectores:
- ¿Cuál es la distribución de las medias muestrales?
- ¿Cuál es la probabilidad de que la media de edad de la muestra esté comprendida entre 16’7 y 17’5 años?
- En una determinada población, los pesos se distribuyen según una normal de media 65 kg. y varianza 49. Si extraemos muestras de tamaño 64, ¿cuál es la probabilidad de que la media de los pesos de una de esas muestras sea mayor que 66’5 kg?
- La edad de los miembros de una determinada asociación se distribuye normalmente con media 52 años y desviación típica 3 años.
- ¿Cuál es la probabilidad de que un miembro elegido al azar sea mayor de 60 años?
- Si se toman muestras de tamaño 36, ¿Cuál es la probabilidad de que la edad media de dichas muestras sea superior a los 60 años?
- La edad de los alumnos de 2º Bachillerato de cierto instituto sigue una distribución N(17’6 , 0’5). Los agrupamos al azar de 10 en 10 para una competición. ¿Cuál es la probabilidad de que en uno de esos grupos la edad media esté comprendida en el intervalo (17,18)?
Método CHIO
“Utilizando las propiedades de los determinantes se trata de hacer ceros a todos los elementos de una línea para luego desarrollarlo por los adjuntos de esa línea”
Ejemplo
\( \left| \begin{array}{cccc} 1 & 2 & 3 & 4 \\ -1 & 0 & 1 & 2 \\ 2 & 0 & 1 & 1 \\ 2 & 2 & -2 & 3 \end{array} \right| \) \( \stackrel{F_4-F_1}{=} \left| \begin{array}{cccc} 1 & 2 & 3 & 4 \\ -1 & 0 & 1 & 2 \\ 2 & 0 & 1 & 1 \\ 1 & 0 & -5 & -1 \end{array} \right| = \stackrel{Desarrollo \, \\ por\, C2}{=} 2(-1)^{1+2}\left| \begin{array}{ccc} -1 & 1 & 2 \\ 2& 1 & 1 \\ 1 & -5 & -1 \end{array} \right| \stackrel{F_1 \leftrightarrow F_3}{=} 2 \cdot \left| \begin{array}{ccc} 1 & -5 & -1 \\ 2& 1 & 1 \\-1 & 1 & 2 \end{array} \right| \)
\( \stackrel{F_2-2F_1\\F_3+F_1}{=}2 \cdot \left| \begin{array}{ccc} 1 & -5 & -1 \\ 0& 11 & 3 \\0& -4 & 1 \end{array} \right| = \stackrel{Desarrollo \\ \,por\, C1} {=} 2 \cdot \left| \begin{array}{cc} 11 & 3 \\ -4& 1 \end{array} \right|=2(11-(-12))=46 \)
Método de GAUSS
“Utilizando las propiedades de los determinantes se trata de conseguir un determinante triangular (superior o inferior) de tal manera que su determinante sea el producto de los elementos de la diagonal”
Ejemplo
\( \left| \begin{array}{cccc} 1 & 2 & 3 \\ -1 & 2 & 4 \\ 1 & 4 & 1 \end{array} \right| \) \( \stackrel{F_2+F_1\\F_3-F_1}{=} \left| \begin{array}{cccc} 1 & 2 & 3 \\ 0 & 4 & 7 \\ 0 & 2 & -2 \end{array} \right| = \stackrel{3F_3}{=} \frac{1}{2}\left| \begin{array}{ccc} 1 & 2 & 3 \\ 0& 4 & 7 \\ 0 & 4& -4 \end{array} \right| \stackrel{F_3-F_2}{=} \frac{1}{2} \cdot \left| \begin{array}{ccc} 1 & 2 & 3\\ 0& 4 & 7 \\0 & 0 & -11 \end{array} \right|=\frac{1}{2}1 \cdot 4 \cdot (-11)=-22 \)
Ejemplo
> \( \left| \begin{array}{cccc} 3 & x & x& x \\ x & 3 & x & x \\ x & x & 3 & x \\ x & x & x & 3 \end{array} \right| \) \( \stackrel{c_1+c_2+c_3+c_4}{=} \left| \begin{array}{cccc} 3x+3 & x & x& x \\ 3x+3 & 3 & x & x \\ 3x+3 & x & 3 & x \\ 3x+3 & x & x & 3 \end{array} \right| = (3x+3)\cdot \left| \begin{array}{cccc} 1 & x & x& x \\ 1 & 3 & x & 1 \\ 1 & x & 3 & x \\ 1 & x & x & 3 \end{array} \right| \stackrel{f_2-f_1\\f_3-f_1\\f_3-f_1}{=} (3x+3)\cdot \left| \begin{array}{cccc} 1 & x & x& x \\ 0 & 3-x & 0 & 0 \\ 0 & 0 & 3-x & 0 \\ 0 & 0 & 0 & 3-x \end{array} \right|=(3x+3)(3-x )^3 \)
Rango de una matriz
Recordemos que el rango de una matriz es el número de filas o columnas linealmente independientes.
Además sabemos que el número de filas L.I. es igual al número de columnas L.I.
Existen fundamentalmente dos métodos para realizarlo: Método de Gauss, Método del Orlado
Método de Gauss
Ya lo hemos visto.
Cálculo por determinantes. Método del orlado
Introducción:
Consideramos una matriz \(A \in Mmxn \) , supongamos que m≤n ( esta restricción no resta generalidad), si tomamos todos los determinantes de las submatrices de orden m (menores de orden m) y vemos que se anulan, podemos deducir que a la fuerza existe una combinación lineal entre sus filas o bien sus columnas.
Dando la vuelta a esta deducción podemos decir que si una matriz \(A \in Mmxn \) (m≤n) existe algún determinante de orden m no nulo, todas las filas y columnas son linealmente independientes \( \iff \) ran(A)=m.
Definición: Sea \( A \in Mmxn \) si en esta matriz se prescinde de una o varias filas o columnas de forma que quede una matriz cuadrada de pxp, el determinante correspondiente se llama menor de la matriz A de orden p.
Definición:
Sea \( A \in Mmxn \) se dice que el rango de A, ran(A), es K, si existe por lo menos un menor de orden K no nulo siendo nulos todos los menores de orden superior a K. (El orden del mayor menor no nulo da el rango de la matriz)
A partir de aquí vamos a ver el método práctico del Orlado para el cálculo de rangos.
Definición
Sea \( A \in Mmxn \) y elegido en ella un menor de orden K, se entenderá por orlar dicho menor, al formar otro menor de orden K+1 añadiendo al primero los elementos de una fila y una columna que no formen parte del menor dado.
Se puede demostrar que “si orlando un menor de orden K distinto de cero todos los determinantes de orden K+1 que se pueden formar son nulos entonces cualquier otro menor de orden superior a K es también nulo, y por lo tanto el rango de A es K”
Nota importante: según lo anteriormente expuesto si tenemos una matriz cuadrada de orden n, talque su determinante sea no nulo entonces su rango es n.
En la práctica para calcular el rango de una matriz se busca un menor de orden 2 no nulo.
>Se elige una columna y se orla con las filas restantes:
- Si todos los orlados son nulos se suprime la columna y se repite la operación con otra columna.
- Si hay un orlado no nulo comenzamos de nuevo y lo orlamos igual que el anterior. El proceso termina cuando no quedan columnas.
Ejemplo
- Calcular el rango de \( \left( \begin{array}{cccc} 1 & 2 & -1& 2 \\ 2 & 1 & 0 & 1 \\ 4 & 5 & -2 & 5 \\ 2 & -1 & 1 & 2 \end{array} \right) \)
Como es una matriz cuadrada primero calcularemos su determinante para ver si su rango es 4. Vemos que |A|= 0 por tanto su \( ran(A) \neq 4 \) .
Seguidamente consideramos un menor de orden 2 no nulo por ejemplo: \( \left| \begin{array}{cccc} 1 & 2 \\ 2 & 1 \end{array} \right| =-3 \neq 0 \)
Orlamos por la siguiente columna:
\( \left| \begin{array}{cccc} 1 & 2 &-1 \\ 2 & 1 &0 \\4&5&-2 \end{array} \right|=0 \) cambiamos de fila \( \left| \begin{array}{cccc} 1 & 2 &-1 \\ 2 & 1 &0 \\2&-1&1 \end{array} \right|=1 \neq 0 \rightarrow \) \(ran(A)\geq 3 \) y como \(|A| =0 \rightarrow ran(A)=3\)
Matriz inversa
En el tema anterior (matrices) se ha visto el concepto de la matriz inversa de una matriz cuadrada y se han calculado inversas de matrices de orden 2 y 3 mediante sistemas de ecuaciones o con el método de Gauss–Jordan. En este apartado veremos una tercera forma de calcular matrices inversas.
Recordemos que una matriz cuadrada A se llama regular (o inversible) si existe otra matriz cuadrada, llamada inversa y que se representa por \( A ^{–1} \) , que multiplicada por la matriz A nos da la matriz identidad.
\( A · A^{-1} = A ^{− 1} · A = I \)
Vamos a deducir cómo es la matriz inversa. Supongamos una matriz cuadrada A de orden n, aunque para facilitar los cálculos trabajaremos con una matriz de orden 3. \( A=\left(\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{array}\right) = \)
Hallamos la traspuesta de la matriz adjunta: \( [Adj(A)]^t=\left(\begin{array}{ccc} A_{11} & A_{21} & A_{31}\\ A_{12} & A_{22} & A_{32}\\ A_{13} & A_{23} & A_{33}\\ \end{array}\right) = \)
Multiplicando la matriz A por la traspuesta de su adjunta \( [ Adj ( A ) ] ^t \) tenemos: \( A=\left(\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{array}\right) \cdot \left(\begin{array}{ccc} A_{11} & A_{21} & A_{31}\\ A_{12} & A_{22} & A_{32}\\ A_{13} & A_{23} & A_{33}\\ \end{array} \right) =\left(\begin{array}{ccc} |A| & 0 & 0\\ 0 & |A| &\\ 0 & 0 & |A|\\ \end{array}\right) =|A| \cdot \left(\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1&0\\ 0 & 0 & 1\\ \end{array}\right)=|A|\cdot I\)
Es decir, al multiplicar A por la traspuesta de su adjunta nos ha aparecido la matriz unidad:
\( A · [ Adj ( A ) ]^t = |A| ⋅ I) \rightarrow A \cdot \frac{1}{|A|} [ Adj ( A ) ]^t =I \)
De donde se deduce que, si el determinante de A no es nulo:
\( A^{-1}= \frac{1}{|A|} [ Adj ( A ) ]^t \)
Como de toda matriz cuadrada se puede hallar su adjunta y luego la traspuesta de ésta, lo único que puede hacer que no exista la inversa es que no exista el factor \( \frac{1}{|A|} \) , que no existe cuando A = 0 .
Luego:
“La condición necesaria y suficiente para una matriz cuadrada tenga inversa es que su determinante sea distinto de cero”
Ejemplo
Calcular la matriz inversa de \(\left(\begin{array}{ccc} 2 & 1 & 0\\ 1 & 1 &-1\\ 1 & 0 & 3\\ \end{array}\right) \)
Primero tenemos que hallar |A| para ver si es inversible o no:
\( |A|=2 \neq 0 \rightarrow A \, es \, inversible \, ó \, regular \)
Calculamos Adj(A)
\( A_{11}=(-1)^{1+1}\left|\begin{array}{ccc} 1 & -1\\ 0 & 3 \end{array}\right| =3 \) \( A_{12}=(-1)^{1+2}\left|\begin{array}{ccc} 1 & -1\\ 1 & 3 \end{array}\right| =-4 \) \( A_{13}=(-1)^{1+3}\left|\begin{array}{ccc} 1 & 1\\ 1 & 0 \end{array}\right| =-1 \) \( A_{21}=(-1)^{2+1}\left|\begin{array}{ccc} 1 & 0\\ 0 & 3 \end{array}\right| =-3 \) \( A_{22}=(-1)^{2+2}\left|\begin{array}{ccc} 2 & 0\\ 1 & 3 \end{array}\right| =6 \) \( A_{23}=(-1)^{2+3}\left|\begin{array}{ccc} 2 & 1\\ 1 & 0 \end{array}\right| =1 \) \( A_{31}=(-1)^{3+1}\left|\begin{array}{ccc} 1 & 0\\ 1 & -1 \end{array}\right| =-1 \) \( A_{32}=(-1)^{3+2}\left|\begin{array}{ccc} 2 & 0\\ 1 & -1 \end{array}\right| =2 \) \( A_{33}=(-1)^{3+3}\left|\begin{array}{ccc} 2 & 1\\ 1 & 1 \end{array}\right| =1 \)
\( Adj(A)=\left(\begin{array}{ccc} 3 & -4 & -1\\ -3 & 6 &1\\ -1 & 2 & 1\\ \end{array}\right) \rightarrow [Adj(A)]^t=\left( \begin{array}{ccc} 3 & -3 & -1\\ -4 & 6 &2\\ -1 & 1 & 1\\ \end{array}\right) \)
\( A^{-1}=\frac{[Adj(A)]^t}{|A|}=\frac{1}{2} \left(\begin{array}{ccc} 3 & -3 & -1\\ -4 & 6 &2\\ -1 & 1 & 1\\ \end{array}\right) =\left(\begin{array}{ccc} \frac{3}{2} & \frac{-3}{2} & \frac{-1}{2}\\ -2 & 3 &1\\ \frac{-1}{2} & \frac{1}{2} & \frac{1}{2}\\ \end{array}\right) \)