Introducción
La Inferencia Estadística es el procedimiento por medio del cual se llega a conclusiones acerca de una población con base en la información que se obtiene a partir de una muestra seleccionada de esa población
El problema de la inferencia estadística es el inverso a los temas donde lo que buscamos es la probabilidad de que ocurran distintas distribuciones planteadas.
Ahora se trata de :A partir de los datos de muestras representativas se inferirán resultados acerca de la población, como por ejemplo estimar el valor de µ (estimación puntual de µ(media poblacional)).
Por ejemplo si queremos calcular la altura media de todos los alumnos, y para ello tenemos una muestra de n=100. ¿qué valor elegimos como el más aproximado a µ?. Si la media de la muestra es de 165cm, podremos afirmar que es “aproximadamente de 165 cm”. Pero no podemos decir que exactamente el valor de µ es de 165cm, pues generalmente el valor de la media muestral (x)no es exactamente el mismo que la media poblacional(µ). Es por esto que esta ésta estimación se dice estimación puntual.
Los estimadores puntuales sólo dan una idea aproximada del verdadero valor del parámetro a estimar, sin saber cómo de fiable es tal aproximación. La estimación puntual es poco útil, es mucho más interesante obtener un intervalo dentro del cual se tiene cierta confianza (fijada de antemano) de que se encuentre el parámetro que se desee aproximar. Estimar un parámetro poblacional, por ejemplo µ, mediante un intervalo [a,b] con un nivel de confianza 1-α (que se suele dar en tanto por cien) se denomina estimación por intervalo de confianza P(a≤µ≤b)=1-α
Intervalo de confianza
El problema ahora es es siguiente: queremos, a partir de una muestra de tamaño n, estimar el valor de un parámetro de la población dando un intervalo en el que confiamos que esté dicho parámetro.
A este intervalo lo denominamos, intervalo de confianza , y se calcula la probabilidad de que eso ocurra a la que se denomina nivel de confianza .
Antes de concretarse en un valor para una muestra determinada, cualquier estadístico puede ser tratado como una variable aleatoria cuya distribución de probabilidad dependerá de la distribución de la variable que represente el comportamiento de la población objeto de estudio. Parece razonable aprovechar la distribución de probabilidad del estadístico utilizado como estimador puntual de un parámetro para, basándose en ella, llegar a determinar un intervalo de confianza para el parámetro que se desea estimar. El método que se utiliza para la obtención del intervalo se conoce como método del estadístico pivote y consta básicamente de los siguientes pasos:
Vamos a ver un ejemplo directamente. Supongamos que tenemos una población de 10.000 naranjas. Queremos estudiar el peso medio de las naranjas(esa es mi variable X). Una opción bastante aburrida y costosa es pesar toda la población de naranjas, lo cual es inviable.
Sería mejor coger un grupo pequeño al azar de 100 naranjas(por ejemplo) y hacer el cálculo del peso medio de esa muestra (la media de este grupo).
Posteriormente , tomamos ese valor con un margen arriba y abajo de esa media del grupo.(Un Intervalo de Confianza )
Es decir calcular la media del grup0 de 100 y decir más o menos la media de todas las naranjas estarían entre este valor y este otro con un 95% de seguridad o 90 % de seguridad( Esto es precisamente el Intervalo de Confianza y el 95% sería la confianza)
IC para la \( \mu \) con \( \sigma\) conocida
¿Como se calcula?Supongamos que cogemos muestras de 100 naranjas y calculamoss la media (el promedio) del peso de las naranjas de cada grupo.

Tenemos las medias de grupos de 100 naranjas. Si tomamos 100 muestras tenemos 100 grupos de 100 naranjas. Es decir tendrás 100 valores de medias. Estas valores de medias actuan como una nueva variable y las representamos con un histograma y vemos su distribución.
El histograma de las medias es similar a la distribución normal cuando la muestra es más grande que 30.
Se ha visto, por experiencia, que el valor central de las medias es igual al de toda la población.
Pero la dispersión (desviación estándar) es la desviación de la población dividido entre la raiz del número de naranjas (n) de la muestra (100 naranjas en este caso).
- La media de las medias es la media de la población
- La desviación estándar de las medias es la desviación estándar de la población dividido entre la raiz del número de la muestra. (error estándar SE)
O sea, \( \overline{x} \) (media muestral) sigue una distribución normal de media μ y desviación típica \( \frac{σ}{\sqrt{n}}\)
La desviación estándar de la media es el error estándar o error de muestreo. Depende de la cantidad de tornillos de la muestra que escojas para calcular la media.
Como has visto el histograma de las media es normal solo para muestras más grandes que 30. Entonces será válida para n> 30.
En nuestro problema de las naranjas tenemos muestras más grandes que 30. El histograma de las medias será una campana de gauss, es decir, una distribución normal de media μ y desviación típica \( \frac{σ}{\sqrt{n}}\) =>\( \overline{x}\sim N(\mu,\frac{σ}{\sqrt{n}} )\)
El 95% de las medias se encuentra en este intervalo:\( (\overline{x}-1,96\cdot \frac{\sigma}{\sqrt{100}},\overline{x}-1,96\cdot \frac{\sigma}{\sqrt{100}}) \)
¿Cuál es la gracia? No hace falta pesar todas las naranjas. Sólo necesitas coger una muestra pequeñita.
Calculas la media y con la desviación estándar ya sabrás dónde estará la media de todas las naranjas con un 95% de posibilidades.
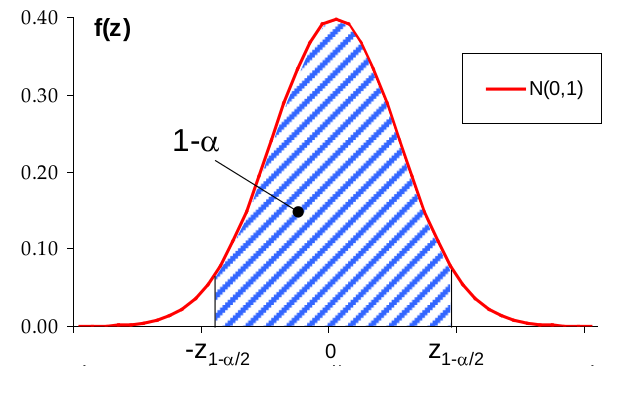
Nota: el 1.96 proviene del 95% por ciento de la normal estándar. Mira esta figura para acordarte:
Proceso general:
Con el fin de estimar µ se toma una muestra aleatoria simple de tamaño n que nos proporciona una media $\overline{x}$, que será el estimador puntual de µ.
Por el teorema central del límite sabemos que la si la población grande, n>30,entonces las medias $\overline{x}$ siguen la ley normal $N(\mu, \frac{\sigma}{\sqrt{n}})$ de forma que la variable tipificada será $z=\frac{\overline{x}-\mu} {\sigma / \sqrt{n}}$ que sigue distribución normal N(0,1).
Si nos dicen el nivel de confianza es 1-α, el intervalo de confianza en Z será: $IC_Z=[-z_{\frac{\alpha}{2}}, z_{\frac{\alpha}{2}} ]$. Siendo $z_{ \alpha/2}$ el valor que cumple $ P(Z \leq Z_{ \frac{\alpha}{2}})=1-\frac{\alpha}{2}.$
conceptos
Intervalo de confianza: Si P ( a ≤ X ≤ b ) = 0 ' 95 tenemos el intervalo de confianza (a, b)
Nivel de confianza o coeficiente de confianza: 1 − α = γ, en nuestro ejemplo, 0’95
Nivel de significación o de riesgo: α, en nuestro ejemplo, 0’05
Valor crítico: k 1 y k 2 , que dejan a la derecha (o a la izquierda) un área α/2.
En la N(0, 1) son −1’96 y 1’96 para α = 0’05.
Margen de error: Diferencia entre los extremos del intervalo de confianza.
Máximo error admisible: Valor prefijado que no puede superar el valor absoluto de la diferencia entre el estimador y el parámetro.
Ejemplo
Se trata de encontrar un intervalo de confianza del 95% para estimar el gasto en transporte de una determinada empresa, gasto que sabemos se distribuye de forma normal de media µ y desviación típica 300.
Para ello se toma una muestra aleatoria simple de tamaño 100, por ejemplo, y utilizamos la media muestral como el mejor estimador de la media poblacional que sabemos que se distribuye \( \overline{x}\sim N(\mu,\frac{300}{\sqrt{100}}) \sim N(\mu,30))\) o, lo que es lo mismo, \( Z= \frac{\overline {X}-\mu} {30} \sim N ( 0,1) \)
Entonces buscamos dos valores a y b tales que \(P ( a \leq \frac{\overline{X}-\mu}{30} \leq b)=0,95 \) y observamos que, para que el intervalo sea lo más estrecho posible, es necesario que a = -b O sea, que \( a=-z_{\alpha/2}=-1,96\) y \( b=z_{\alpha/2}=1,96\) con lo que \(P ( -1.96 \leq \frac{\overline{X}-\mu}{30} \leq 1.96)=0,95 \) que despejando µ se obtiene \(P ( -1.9630+ \overline{X} \leq \mu \leq 1.96+ \overline{X})=0,95 =1-\alpha\)
O sea \(P ( \overline{X} -58.8 \leq -\mu \leq \overline{X}+58.8)=0,95 \) que quiere decir que hemos encontrado dos estimadores \( (\overline{X}-58.8,\overline{X}+58.8) \) y tales que \( P(\overline{X}-58.8 \leq \mu \leq \overline{X}+58.8) =0,95\)
Ejercicios
Determina un intervalo de confianza con un nivel de confianza del 95 % de una N(6, 0’01). Determina el margen de error.
Determina un intervalo de confianza con un nivel de confianza del 99 % de una N(100, 3). Determina el margen de error.
Intervalos de confianza para proporciones
En la inferencia sobre una proporción el problema se concreta en estimar y contrastar la proporción p de individuos de una población que presentan una determinada característica A (proporción de votantes a un partido político, proporción de parados, ...).
El problema se modeliza mediante una variable dicotómica que toma el valor 1 si se presenta la característica de interés y 0 en caso contrario, esto es, una variable de Bernoulli, \(X \sim B(p)\),de la que se dispone de una muestra de tamaño n. Entonces, la proporción poblacional p no es otra cosa que la media poblacional de dicha variable, estimándose con la correspondiente proporción muestral o media muestral, \( \hat p \sim \overline {X} \) .
La construcción de un intervalo de confianza para la proporción de éxitos en una prueba de Bernoulli se puede llevar a cabo utilizando el estimador puntual . \( \hat p \sim \ N(p,\sqrt{\frac{p(1-p)}{n}})) \) para nsuficientemente grande
Tipificando la variable obtenemos una distribución N(0, 1), por lo tanto: \( \frac{\overline{X}-p}{\sqrt{p(1-p)}}\sim N(0,1)\)
Dado un nivel de confianza 1 − α , se deben buscar dos valores \(z_{ 1- \alpha/2} \hspace{1em} y \hspace{1em} −z_{ 1-\alpha /2}\) que verifiquen: \[ \phi(-z_{1-\alpha/2})=\frac{\alpha}{2} \hspace{1em} y \hspace{1em} \phi(z_{1-\alpha/2})=1-\frac{\alpha}{2}\]
De manera que construimos el intervalo de confianza para la proporción de éxitos p. La varianza es desconocida y por tanto se utiliza como desviación típica su estimador puntual \( \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\) \[ P(-z_{1-\alpha/2}\le \frac{\hat{p}-p }{\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}} \le z_{1-\alpha/2})=1-\alpha \Rightarrow P(-\hat{p}-z_{1-\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\le -p \le -\hat{p} z_{1-\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}})=1-\alpha \] \[ P(\hat{p}-z_{1-\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\le p \le \hat{p} +z_{1-\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}})=1-\alpha \]
Tenemos el intervalo para la proporción poblacional: \[ p \in \left(\hat{p}-z_{1-\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}, \hat{p} +z_{1-\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\right) \]
El determinante de una matriz A es igual al determinante de su traspuesta.
\( |A^t|=\left|\begin{array}{ccc} a_{11} & a_{21} & a_{31}\\ a_{12} & a_{22} & a_{32}\\a_{13} & a_{23} & a_{33}\\ \end{array}\right| = a_{11}a_{ 22}a_{ 33} +a_{21}a_{32}a_{ 13}+ a_{31}a_{ 12}a_{ 23}-( a_{31}a_{ 22}a_{ 13}+ a_{11}a_{ 32}a_{ 23}+a_{21}a_{ 12}a_{ 33} ) \)
Reorganizando
\(
= a_{11}a_{ 22}a_{ 33}+a_{12}a_{ 23}a_{ 31}+a_{13}a_{ 21}a_{ 32}-( a_{11}a_{ 23}a_{ 32}+ a_{12}a_{ 21}a_{ 33}+a_{13}a_{ 22}a_{ 31} )
=|A|
\)
Ejemplo
\( |A|=\left|\begin{array}{ccc} 2 & 3 & 4\\ 1 & 3 & 2\\ 5 & 1 & 0\\ \end{array}\right| = 2 ⋅ 3 ⋅ 0 + 1 ⋅ 1 ⋅ 4 + 3 ⋅ 2 ⋅ 5 − 4 ⋅ 3 ⋅ 5 − 3 ⋅ 1 ⋅ 0 − 2 ⋅ 1 ⋅ 2 = 0 + 4 + 30 − 60 − 0 − 4 = -30 \)
\( |A^t|=\left|\begin{array}{ccc} 2 & 1 & 5\\ 3 & 3 & 1\\ 4 & 2 & 0\\ \end{array}\right| = 2 ⋅ 3 ⋅ 0 + 1 ⋅ 1 ⋅ 4 + 3 ⋅ 2 ⋅ 5 − 4 ⋅ 3 ⋅ 5 − 3 ⋅ 1 ⋅ 0 − 2 ⋅ 1 ⋅ 2 = 0 + 4 + 30 − 60 − 0 − 4 = − 30 \)
Considerando entonces esta propiedad, todo los resultado para la filas de un determinante será igualmente válido para las columnas, y viceversa, pudiendo hablar simplemente de líneas de un determinante.
Si los elementos de una fila o de una columna se multiplican todos por un número, el determinante queda multiplicado por dicho número.
\( A=\left|\begin{array}{ccc} ka_{11} & a_{12} & a_{13}\\ ka_{21} & a_{22} & a_{23}\\ ka_{31} & a_{32} & a_{33}\\ \end{array}\right| = ka_{11}a_{ 22}a_{ 33}+ka_{12}a_{ 23}a_{ 31}+ka_{13}a_{ 21}a_{ 32}-( ka_{11}a_{ 23}a_{ 32}+ ka_{12}a_{ 21}a_{ 33}+ka_{13}a_{ 22}a_{ 31} ) =k(a_{11}a_{ 22}a_{ 33}+a_{12}a_{ 23}a_{ 31}+a_{13}a_{ 21}a_{ 32}-( a_{11}a_{ 23}a_{ 32}+ a_{12}a_{ 21}a_{ 33}+a_{13}a_{ 22}a_{ 31} ) )=k \cdot \left|\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{array}\right| \)
Por lo tanto, esta propiedad
- Nos permite sacar fuera los factores comunes a todos los elementos de una línea.
- \(|k · A| = k^n · |A|\), siendo n la dimensión de la matriz
\( |A|= \left|\begin{array}{ccc} ka_{11} & ka_{12} & ka_{13}\\ ka_{21} & ka_{22} & ka_{23}\\ ka_{31} & ka_{32} & ka_{33}\\ \end{array}\right| = =k \cdot \left|\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ ka_{21} & ka_{22} & ka_{23}\\ ka_{31} & ka_{32} & ka_{33}\\ \end{array}\right| =k^2 \left|\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ ka_{31} & ka_{32} & ka_{33}\\ \end{array}\right|=k^3 \left|\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{array}\right| =k^3 |A| \)
Si los elementos de una línea se pueden descomponer en suma de dos o más sumandos, el determinante será igual a la suma de dos determinantes (o más) que tienen todas las restantes líneas iguales y en dicha línea tienen los primeros, segundos, etc. sumandos.
\( \left|\begin{array}{ccc} a_{11}+b_{11}& a_{12} & a_{13}\\ a_{21} +b_{21} & a_{22} & a_{23}\\ a_{31}+b_{31} & a_{32} & a_{33}\\ \end{array}\right| = \left|\begin{array}{ccc} a_{11}& a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{array}\right|+ \left|\begin{array}{ccc} b_{11}& a_{12} & a_{13}\\ b_{21} & a_{22} & a_{23}\\ b_{31} & a_{32} & a_{33}\\ \end{array}\right| \)
Si en un determinante los elemento de una línea son nulos, el determinante es nulo.
\( |A|=\left|\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ 0 & 0& 0\\ a_{31} & a_{32} & a_{33}\\ \end{array}\right| = a_{11}\cdot 0\cdot a_{ 33} + 0\cdot a_{32}a_{ 13}+ a_{31}a_{ 12}\cdot 0-( a_{31}\cdot 0\cdot a_{ 13}+ a_{11}a_{ 32}\cdot 0+0\cdot a_{ 12}a_{ 33} ) =0 \)
Si en una matriz se permutan dos filas (o dos columnas), el determinante cambia de signo.
\( | A|=\left|\begin{array}{ccc} a_{21} & a_{22} & a_{23}\\a_{11} & a_{12} & a_{13}\\ a_{31} & a_{32} & a_{33}\\ \end{array}\right| =-\left|\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{array}\right| =- | A| \)
Ejemplo
\( \left|\begin{array}{ccc} 2 & 3 & 4\\ 1 & 3 & 2\\ 5 & 1 & 0\\ \end{array}\right| = -30 \)
\( \left|\begin{array}{ccc} 1 & 3 & 2\\ 2 & 3 & 4\\ 5 & 1 & 0\\ \end{array}\right| = 30 \)
Si un determinante tiene dos líneas paralelas iguales, el determinante es nulo.
\( | A|=\left|\begin{array}{ccc} a_{11} & a & a\\ a_{21} & b & b\\ a_{31} & c & c\\ \end{array}\right| = = a_{11}bc +a_{31}ab+ a_{21}ac-( aba_{ 31}+ a_{11}cb+a_{21}ac )=0 \)
Si una matriz cuadrada tiene dos filas o dos columnas proporcionales, su determinante es nulo.
\( |A|=\left|\begin{array}{ccc} a_{11} & ka_{11} & a_{13}\\ a_{21} & ka_{21} & a_{23}\\ a_{31} & ka_{31} & a_{33}\\ \end{array}\right| = k \cdot \left|\begin{array}{ccc} a_{11} & a_{11} & a_{13}\\ a_{21} & a_{21} & a_{23}\\ a_{31} & a_{31} & a_{33}\\ \end{array}\right|=k \cdot 0=0 \)
ya que una matriz con dos filas iguales tiene determinante 0
Si los elementos de una línea son combinación lineal de las restantes líneas paralelas, el determinante es nulo.
\( |A|=\left|\begin{array}{ccc} a_{11} & a_{12} & r · a_{11}+s · a_{12}\\ a_{21} & a_{22} & r · a_{21}+s · a_{22}\\ a_{31} & a_{32} & r · a_{31}+s · a_{32}\\ \end{array}\right| = \left|\begin{array}{ccc} a_{11} & a_{12} & r · a_{11}\\ a_{21} & a_{22} & r · a_{21}\\ a_{31} & a_{32} & r · a_{31}\\ \end{array}\right| +\left|\begin{array}{ccc} a_{11} & a_{11} & s · a_{12}\\ a_{21} & a_{21} &s · a_{22}\\ a_{31} & a_{31} & s · a_{32}\\ \end{array}\right|=r \cdot \left|\begin{array}{ccc} a_{11} & a_{12} & a_{11}\\ a_{21} & a_{22} & a_{21}\\ a_{31} & a_{32} & a_{31}\\ \end{array}\right| +s \cdot \left|\begin{array}{ccc} a_{11} & a_{12} & a_{12}\\ a_{21} & a_{22} & a_{22}\\ a_{31} & a_{32} & s · a_{32}\\ \end{array}\right|=r \cdot 0 +s \cdot 0 =0 \)Si a los elementos de una línea se le suma una combinación lineal de las restantes líneas paralelas,el determinante no varía.
\( \left|\begin{array}{ccc} a_{11} & a_{12} & a_{13}+r · a_{11}+s · a_{12}\\ a_{21} & a_{22} & a_{23}+r · a_{21}+s · a_{22}\\ a_{31} & a_{32} & a_{33}+r · a_{31}+s · a_{32}\\ \end{array}\right| = \left|\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{array}\right| + \left|\begin{array}{ccc} a_{11} & a_{12} & r · a_{11}\\ a_{21} & a_{22} & r · a_{21}\\ a_{31} & a_{32} & r · a_{31}\\ \end{array}\right| + \left|\begin{array}{ccc} a_{11} & a_{12} & s · a_{12}\\ a_{21} & a_{22} &s · a_{22}\\ a_{31} & a_{32} & s · a_{32}\\ \end{array}\right|= \)
\( \left|\begin{array}{ccc} a_{11} & a_{12} & r · a_{11}\\ a_{21} & a_{22} & r · a_{21}\\ a_{31} & a_{32} & r · a_{31}\\ \end{array}\right|+ r \cdot \left|\begin{array}{ccc} a_{11} & a_{12} & a_{11}\\ a_{21} & a_{22} & a_{21}\\ a_{31} & a_{32} & a_{31}\\ \end{array}\right| +s \cdot \left|\begin{array}{ccc} a_{11} & a_{12} & a_{12}\\ a_{21} & a_{22} & a_{22}\\ a_{31} & a_{32} & a_{32}\\ \end{array}\right|=\left|\begin{array}{ccc} a_{11} & a_{12} & r · a_{11}\\ a_{21} & a_{22} & r · a_{21}\\ a_{31} & a_{32} & r · a_{31}\\ \end{array}\right|+r \cdot 0 +s \cdot 0 =\left|\begin{array}{ccc} a_{11} & a_{12} & r · a_{11}\\ a_{21} & a_{22} & r · a_{21}\\ a_{31} & a_{32} & r · a_{31}\\ \end{array}\right| \)
El determinante del producto de dos matrices cuadradas es igual al producto de los determinantes de las matrices:.
\( |A \cdot B|=|A| \cdot |B| \)
Método CHIO
“Utilizando las propiedades de los determinantes se trata de hacer ceros a todos los elementos de una línea para luego desarrollarlo por los adjuntos de esa línea”
Ejemplo
\( \left| \begin{array}{cccc} 1 & 2 & 3 & 4 \\ -1 & 0 & 1 & 2 \\ 2 & 0 & 1 & 1 \\ 2 & 2 & -2 & 3 \end{array} \right| \) \( \stackrel{F_4-F_1}{=} \left| \begin{array}{cccc} 1 & 2 & 3 & 4 \\ -1 & 0 & 1 & 2 \\ 2 & 0 & 1 & 1 \\ 1 & 0 & -5 & -1 \end{array} \right| = \stackrel{Desarrollo \, \\ por\, C2}{=} 2(-1)^{1+2}\left| \begin{array}{ccc} -1 & 1 & 2 \\ 2& 1 & 1 \\ 1 & -5 & -1 \end{array} \right| \stackrel{F_1 \leftrightarrow F_3}{=} 2 \cdot \left| \begin{array}{ccc} 1 & -5 & -1 \\ 2& 1 & 1 \\-1 & 1 & 2 \end{array} \right| \)
\( \stackrel{F_2-2F_1\\F_3+F_1}{=}2 \cdot \left| \begin{array}{ccc} 1 & -5 & -1 \\ 0& 11 & 3 \\0& -4 & 1 \end{array} \right| = \stackrel{Desarrollo \\ \,por\, C1} {=} 2 \cdot \left| \begin{array}{cc} 11 & 3 \\ -4& 1 \end{array} \right|=2(11-(-12))=46 \)
Método de GAUSS
“Utilizando las propiedades de los determinantes se trata de conseguir un determinante triangular (superior o inferior) de tal manera que su determinante sea el producto de los elementos de la diagonal”
Ejemplo
\( \left| \begin{array}{cccc} 1 & 2 & 3 \\ -1 & 2 & 4 \\ 1 & 4 & 1 \end{array} \right| \) \( \stackrel{F_2+F_1\\F_3-F_1}{=} \left| \begin{array}{cccc} 1 & 2 & 3 \\ 0 & 4 & 7 \\ 0 & 2 & -2 \end{array} \right| = \stackrel{3F_3}{=} \frac{1}{2}\left| \begin{array}{ccc} 1 & 2 & 3 \\ 0& 4 & 7 \\ 0 & 4& -4 \end{array} \right| \stackrel{F_3-F_2}{=} \frac{1}{2} \cdot \left| \begin{array}{ccc} 1 & 2 & 3\\ 0& 4 & 7 \\0 & 0 & -11 \end{array} \right|=\frac{1}{2}1 \cdot 4 \cdot (-11)=-22 \)
Ejemplo
> \( \left| \begin{array}{cccc} 3 & x & x& x \\ x & 3 & x & x \\ x & x & 3 & x \\ x & x & x & 3 \end{array} \right| \) \( \stackrel{c_1+c_2+c_3+c_4}{=} \left| \begin{array}{cccc} 3x+3 & x & x& x \\ 3x+3 & 3 & x & x \\ 3x+3 & x & 3 & x \\ 3x+3 & x & x & 3 \end{array} \right| = (3x+3)\cdot \left| \begin{array}{cccc} 1 & x & x& x \\ 1 & 3 & x & 1 \\ 1 & x & 3 & x \\ 1 & x & x & 3 \end{array} \right| \stackrel{f_2-f_1\\f_3-f_1\\f_3-f_1}{=} (3x+3)\cdot \left| \begin{array}{cccc} 1 & x & x& x \\ 0 & 3-x & 0 & 0 \\ 0 & 0 & 3-x & 0 \\ 0 & 0 & 0 & 3-x \end{array} \right|=(3x+3)(3-x )^3 \)
Rango de una matriz
Recordemos que el rango de una matriz es el número de filas o columnas linealmente independientes.
Además sabemos que el número de filas L.I. es igual al número de columnas L.I.
Existen fundamentalmente dos métodos para realizarlo: Método de Gauss, Método del Orlado
Método de Gauss
Ya lo hemos visto.
Cálculo por determinantes. Método del orlado
Introducción:
Consideramos una matriz \(A \in Mmxn \) , supongamos que m≤n ( esta restricción no resta generalidad), si tomamos todos los determinantes de las submatrices de orden m (menores de orden m) y vemos que se anulan, podemos deducir que a la fuerza existe una combinación lineal entre sus filas o bien sus columnas.
Dando la vuelta a esta deducción podemos decir que si una matriz \(A \in Mmxn \) (m≤n) existe algún determinante de orden m no nulo, todas las filas y columnas son linealmente independientes \( \iff \) ran(A)=m.
Definición: Sea \( A \in Mmxn \) si en esta matriz se prescinde de una o varias filas o columnas de forma que quede una matriz cuadrada de pxp, el determinante correspondiente se llama menor de la matriz A de orden p.
Definición:
Sea \( A \in Mmxn \) se dice que el rango de A, ran(A), es K, si existe por lo menos un menor de orden K no nulo siendo nulos todos los menores de orden superior a K. (El orden del mayor menor no nulo da el rango de la matriz)
A partir de aquí vamos a ver el método práctico del Orlado para el cálculo de rangos.
Definición
Sea \( A \in Mmxn \) y elegido en ella un menor de orden K, se entenderá por orlar dicho menor, al formar otro menor de orden K+1 añadiendo al primero los elementos de una fila y una columna que no formen parte del menor dado.
Se puede demostrar que “si orlando un menor de orden K distinto de cero todos los determinantes de orden K+1 que se pueden formar son nulos entonces cualquier otro menor de orden superior a K es también nulo, y por lo tanto el rango de A es K”
Nota importante: según lo anteriormente expuesto si tenemos una matriz cuadrada de orden n, talque su determinante sea no nulo entonces su rango es n.
En la práctica para calcular el rango de una matriz se busca un menor de orden 2 no nulo.
>Se elige una columna y se orla con las filas restantes:
- Si todos los orlados son nulos se suprime la columna y se repite la operación con otra columna.
- Si hay un orlado no nulo comenzamos de nuevo y lo orlamos igual que el anterior. El proceso termina cuando no quedan columnas.
Ejemplo
- Calcular el rango de \( \left( \begin{array}{cccc} 1 & 2 & -1& 2 \\ 2 & 1 & 0 & 1 \\ 4 & 5 & -2 & 5 \\ 2 & -1 & 1 & 2 \end{array} \right) \)
Como es una matriz cuadrada primero calcularemos su determinante para ver si su rango es 4. Vemos que |A|= 0 por tanto su \( ran(A) \neq 4 \) .
Seguidamente consideramos un menor de orden 2 no nulo por ejemplo: \( \left| \begin{array}{cccc} 1 & 2 \\ 2 & 1 \end{array} \right| =-3 \neq 0 \)
Orlamos por la siguiente columna:
\( \left| \begin{array}{cccc} 1 & 2 &-1 \\ 2 & 1 &0 \\4&5&-2 \end{array} \right|=0 \) cambiamos de fila \( \left| \begin{array}{cccc} 1 & 2 &-1 \\ 2 & 1 &0 \\2&-1&1 \end{array} \right|=1 \neq 0 \rightarrow \) \(ran(A)\geq 3 \) y como \(|A| =0 \rightarrow ran(A)=3\)
Matriz inversa
En el tema anterior (matrices) se ha visto el concepto de la matriz inversa de una matriz cuadrada y se han calculado inversas de matrices de orden 2 y 3 mediante sistemas de ecuaciones o con el método de Gauss–Jordan. En este apartado veremos una tercera forma de calcular matrices inversas.
Recordemos que una matriz cuadrada A se llama regular (o inversible) si existe otra matriz cuadrada, llamada inversa y que se representa por \( A ^{–1} \) , que multiplicada por la matriz A nos da la matriz identidad.
\( A · A^{-1} = A ^{− 1} · A = I \)
Vamos a deducir cómo es la matriz inversa. Supongamos una matriz cuadrada A de orden n, aunque para facilitar los cálculos trabajaremos con una matriz de orden 3. \( A=\left(\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{array}\right) = \)
Hallamos la traspuesta de la matriz adjunta: \( [Adj(A)]^t=\left(\begin{array}{ccc} A_{11} & A_{21} & A_{31}\\ A_{12} & A_{22} & A_{32}\\ A_{13} & A_{23} & A_{33}\\ \end{array}\right) = \)
Multiplicando la matriz A por la traspuesta de su adjunta \( [ Adj ( A ) ] ^t \) tenemos: \( A=\left(\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{array}\right) \cdot \left(\begin{array}{ccc} A_{11} & A_{21} & A_{31}\\ A_{12} & A_{22} & A_{32}\\ A_{13} & A_{23} & A_{33}\\ \end{array} \right) =\left(\begin{array}{ccc} |A| & 0 & 0\\ 0 & |A| &\\ 0 & 0 & |A|\\ \end{array}\right) =|A| \cdot \left(\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1&0\\ 0 & 0 & 1\\ \end{array}\right)=|A|\cdot I\)
Es decir, al multiplicar A por la traspuesta de su adjunta nos ha aparecido la matriz unidad:
\( A · [ Adj ( A ) ]^t = |A| ⋅ I) \rightarrow A \cdot \frac{1}{|A|} [ Adj ( A ) ]^t =I \)
De donde se deduce que, si el determinante de A no es nulo:
\( A^{-1}= \frac{1}{|A|} [ Adj ( A ) ]^t \)
Como de toda matriz cuadrada se puede hallar su adjunta y luego la traspuesta de ésta, lo único que puede hacer que no exista la inversa es que no exista el factor \( \frac{1}{|A|} \) , que no existe cuando A = 0 .
Luego:
“La condición necesaria y suficiente para una matriz cuadrada tenga inversa es que su determinante sea distinto de cero”
Ejemplo
Calcular la matriz inversa de \(\left(\begin{array}{ccc} 2 & 1 & 0\\ 1 & 1 &-1\\ 1 & 0 & 3\\ \end{array}\right) \)
Primero tenemos que hallar |A| para ver si es inversible o no:
\( |A|=2 \neq 0 \rightarrow A \, es \, inversible \, ó \, regular \)
Calculamos Adj(A)
\( A_{11}=(-1)^{1+1}\left|\begin{array}{ccc} 1 & -1\\ 0 & 3 \end{array}\right| =3 \) \( A_{12}=(-1)^{1+2}\left|\begin{array}{ccc} 1 & -1\\ 1 & 3 \end{array}\right| =-4 \) \( A_{13}=(-1)^{1+3}\left|\begin{array}{ccc} 1 & 1\\ 1 & 0 \end{array}\right| =-1 \) \( A_{21}=(-1)^{2+1}\left|\begin{array}{ccc} 1 & 0\\ 0 & 3 \end{array}\right| =-3 \) \( A_{22}=(-1)^{2+2}\left|\begin{array}{ccc} 2 & 0\\ 1 & 3 \end{array}\right| =6 \) \( A_{23}=(-1)^{2+3}\left|\begin{array}{ccc} 2 & 1\\ 1 & 0 \end{array}\right| =1 \) \( A_{31}=(-1)^{3+1}\left|\begin{array}{ccc} 1 & 0\\ 1 & -1 \end{array}\right| =-1 \) \( A_{32}=(-1)^{3+2}\left|\begin{array}{ccc} 2 & 0\\ 1 & -1 \end{array}\right| =2 \) \( A_{33}=(-1)^{3+3}\left|\begin{array}{ccc} 2 & 1\\ 1 & 1 \end{array}\right| =1 \)
\( Adj(A)=\left(\begin{array}{ccc} 3 & -4 & -1\\ -3 & 6 &1\\ -1 & 2 & 1\\ \end{array}\right) \rightarrow [Adj(A)]^t=\left( \begin{array}{ccc} 3 & -3 & -1\\ -4 & 6 &2\\ -1 & 1 & 1\\ \end{array}\right) \)
\( A^{-1}=\frac{[Adj(A)]^t}{|A|}=\frac{1}{2} \left(\begin{array}{ccc} 3 & -3 & -1\\ -4 & 6 &2\\ -1 & 1 & 1\\ \end{array}\right) =\left(\begin{array}{ccc} \frac{3}{2} & \frac{-3}{2} & \frac{-1}{2}\\ -2 & 3 &1\\ \frac{-1}{2} & \frac{1}{2} & \frac{1}{2}\\ \end{array}\right) \)