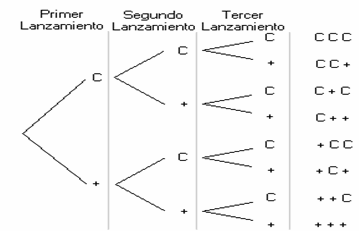
Variaciones sin repetición

Si tenemos una población de tamaño n y queremos extraer una muestra ordenada y sin repetición de tamaño k (k ≤n), razonemos de este modo:

• El primer elemento lo podemos elegir entre n elementos.
• El segundo, al no poder repetir, podemos elegirlo entre n − 1 elementos. (n-2+1) .
• El tercero, al no poder repetir, podemos elegirlo entre n − 2 elementos. (n-3+1) .
• ...
• El elemento k, lo podremos elegir entre n − k + 1 elementos.

Por tanto, y aplicando el principio de multiplicación en total hay : \[ n · (n − 1) · ... · (n − k + 1)\] muestras de tamaño k ordenadas y sin repetición

Las muestras ordenadas y sin repetición se denominan Variaciones sin repetición . Por tanto,si el tamaño de la población es n y el de la muestra k, el número de variaciones sin repetición lo expresaremos por: \[V_n^k = n · (n − 1) · ... · (n − k + 1)\]

Ejercicio

¿Cuántos números de cuatro cifras no repetidas se pueden formar con las cifras del 1 al 9 (ambas inclusive)?

VAriaciones con repetición

>Si la población es de tamaño n y la muestra de tamaño k, pero ahora permitimos repeticiones,procedemos así:

• El primer elemento lo podemos elegir entre n elementos.
• El segundo, al no poder repetir, podemos elegirlo entre n elementos. .
• El tercero, al no poder repetir, podemos elegirlo entre n elementos. .
• ...
• El elemento k, lo podremos elegir entre n elementos.

En total tendremos $n·n·... ·n (k \,veces ) = n^k$ muestras de este tipo.

Las muestras ordenadas y con repetición se denominan Variaciones con repetición y lo expresaremos: \[VR_n^k = n^k\]

Ejemplo

1. ¿De cuántas maneras se pueden elegir 4 cartas (no necesariamente distintas de una baraja de 40 cartas?.

La primera se puede elegir de 40 maneras.

La segunda, al poder repetir, tambi´en se puede elegir de 40 maneras.

La tercera, al poder repetir, tambi´en se puede elegir de 40 maneras.

La cuarta, al poder repetir, tambi´en se puede elegir de 40 maneras.

En total hay 40·40·40·40 = 2560000 formas.

Ejercicio

¿Cuántos números de tres cifras (no necesariamente distintas) pueden formarse con los dígitos 1,6,7,8,9?.

Permutaciones simples o sin repetición

Si tenemos una población de tamaño n y queremos extraer una muestra ordenada y sin repetición de tamaño n, razonemos de este modo:

• El primer elemento lo podemos elegir entre n elementos.
• El segundo, al no poder repetir, podemos elegirlo entre n − 1 elementos. (n-2+1) .
• El tercero, al no poder repetir, podemos elegirlo entre n − 2 elementos. (n-3+1) .
• ...
• El elemento n, lo podremos elegir entre n − n + 1 elementos.(el último)

Es un caso particular de variacionesque se tome una muestra de tamaño igual al tamaño de la población, es decir, k = n, las variaciones se denominan permutaciones y se obtendría: \[V_n^n = n · (n − 1) · ... · (n − n + 1) = n · (n − 1) · ... · 1\]

El producto de todos los números enteros desde el 1 hasta el n se denomina factorial de n y se representa por $n!$. Por definición, 0!=1 y 1!=1. No existen los factoriales de los números negativos

Por tanto este caso particular de variaciones sin repetición se denomina permutaciones sin repetición de n elementos y se expresa: \[P_n = n!\]

Ejemplo

¿De cuántas maneras se pueden sentar 10 alumnos personas en 10 asientos en un aula?. El primer alumno se puede sentar en 10 sitios. El segundo en 9, el tercero en 8, ...etc. De modo que hay 10·9·8·....·3·2·1 = 120 posibilidades, es decir, $P_{10} = 10! =3628800.$

Ejercicio: ¿Cuántas palabras de 8 letras (con o sin sentido) se pueden formar con las letras A B C D E F G H?.

Permutaciones con repetición

Si queremos calcular el número de permutaciones de n elementos de los cuáles hay n1 de una clase,n2 de otra, etc. . . de modo que n1 + n2 + ...+ nr = n , entonces hablamos de permutaciones de n elementos, algunos de los cuales están repetidos, lo que se expresa como: \[P_n^{ n1,n2,...,nr}=\frac{n!}{n1! · n2! · ... · nr !} \]

Ejemplo:

Con los digitos 1 1 1 0 0 ,¿ cuántas cadenas de 5 cifras pueden formarse? La A se repite 3 veces y la letra B se repite 2 veces, y en total hay 5 letras. Así el número total de palabras son:\[ P_5^{3,2}=\frac{5!}{3!\cdot 2!}=\frac{5 · 4 · 3 · 2 · 1}{3 · 2 · 1 · 2 · 1 }=10\]

Dichas palabras serían: 11100, 11010, 11001, 10110, 10101, 10011 ... Escribe los restantes.

Ejercicio:

Con 5 signos + y 3 signos - ¿Cuántas cadenas de símbolos se pueden formar?

Combinaciones

Supongamos que tenemos una bolsa con 5 bolas numeradas del 1 al 5. Sacamos dos bolas, sin importarnos el orden y sin repetir, ¿cuántos posibles resultados hay?. Examinemos las posibilidades. Si el orden fuese importante ya sabemos que tendríamos 5·4 = 20 posibilidades \( ( V_5^2 = 5 · 4)\) que serían:
1, 2         1, 3         1, 4        1, 5
2, 1         2, 3         2, 4         2, 5
3, 1         3, 2         3, 4         3, 5
4, 1         4, 2         4, 3         4, 5
5, 1         5, 2         5, 3         5, 4

> Ahora bien, como no nos importa el orden, para nosotros las parejas 2,1 y 1,2 que son 2, en realidad sólo deberían contar como una, y lo mismo ocurre con el resto de parejas.

Estamos contando cada pareja 2 veces. Por tanto, para obtener el número de parejas que buscamos tenemos que dividir entre 2. Así resulta que el número de muestras no ordenadas y sin repetición que tenemos es de: 20 2 = 10 , sólo 10 posibilidades que son:

{1, 2}, {1, 3}, {1, 4}, {1, 5}, {2, 3}, {2, 4}, {2, 5}, {3, 4}, {3, 5}, {4, 5}

donde las llaves indican que el orden no importa.

Si sacásemos 3 bolas en lugar de 2, tendríamos los tríos: 1,2,3       1,2,4      1,2,5      etc. . . en total 5·4·3 =60 posibilidades \((V_5^3 = 5 · 4 · 3)\).

Razonando de igual manera al caso anterior, todos aquellos tríos en los que estuviesen por ejemplo, el 1, el 2 y el 3 estarían repetidos.

Ahora bien, ¿cuántas veces se repite cada trío?. Veamos, tomando como ejemplo los tríos con 1,2 y 3 obtenemos: 1,2,3       1,3,2     2,1,3      2,3,1      3,1,2      3,2,1 6 posibilidades $(P_3 = 3!)$ que en realidad representan lo mismo pues no nos importa el orden.

Lo mismo ocurre con cada trío, de modo que cada uno de ellos se repite 6 veces, así pu´es si no tenemos en cuenta el orden, el número de muestras no son 60 sino: $\frac{60}{6} = 10$ maneras (no ordenadas y sin repetición).

Ejercicio:

>Escribir los 10 tríos del ejemplo anterior.

> Formalizando lo anterior, si la población es de tamaño n y se extraen muestras de tamaño k, si fuesen ordenadas serían $V_k=n = n · (n − 1) · ... · (n − k + 1)$ pero como son no ordenadas tenemos que dividir por el número de maneras de ordenar esas muestras de tamaño k, es decir hay que dividir por $P_k = k!$

Resumiendo, el número de muestras no ordenadas y sin repetición de tamaño k que se extraen de una población de tamaño n es: \[ \frac{V_n^k}{P_k}\]

Las muestras no ordenadas y sin repetición se denominan Combinaciones sin repetición y las expresaremos:

El número de combinaciones sin repetición $C_n^k$ se recuerda de manera más sencilla mediante otra fórmula: \[ C_n^k=\left(\begin{array}{c}{n} \\ {k}\end{array}\right)\]

La expresión n k se denomina número combinatorio y se lee ”n sobre k”.

Una regla sencilla que permite calcular este número combinatorio es: \[ C_n^k=\left(\begin{array}{c}{n} \\ {k}\end{array}\right)=\frac{n!}{(n-k)! \cdot k!}\]

Ejemplos:

>1. ¿De cuántas maneras se pueden sacar 3 bolas numeradas en cualquier orden, de una bolsa que contiene 5 bolas?.

Serían combinaciones de 5 elementos de los que sacamos 3, es decir, tenemos que calcular: \[ C_5^3=\left(\begin{array}{c}{5} \\ {3}\end{array}\right)=\frac{5!}{(5-3)! \cdot 3!}=10\] son las maneras que habíamos calculado en el ejemplo de la introducción.

2. ¿De cuántas formas se puede formar un grupo de trabajo de 6 alumnos de entre una clase de 27?.

En este caso son combinaciones (no importa el orden ) de 27 elementos de los que se escogen 6 , es decir: \[ C_{27}^6=\left(\begin{array}{c}{27} \\ {6}\end{array}\right)=\frac{27!}{(21)! \cdot 6!}=296010\]C6

Ejercicio: ¿De cuántas maneras se pueden extraer 6 bolas de un bombo que contiene 49 bolas?(Lotería Primitiva)